[最も欲しかった] 因数分解 公式 3 乗 176832
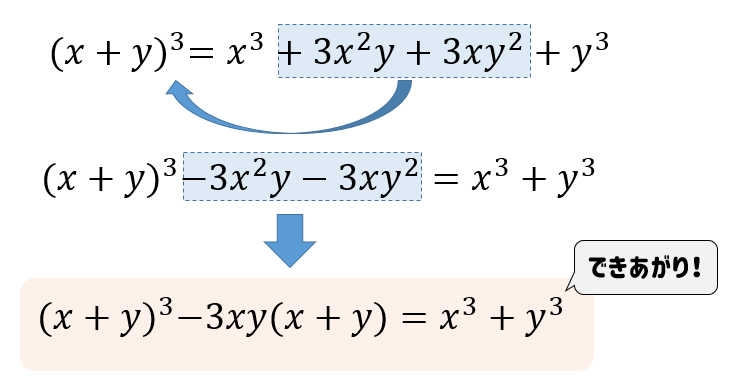
二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ
確認まずは、後で使う2次と3次の因数分解の公式を確認しておきましょう。2次の因数分解の公式平方の差の因数分解公式: 3次の因数分解の公式立方の和と差の因数分解公式: 6次の因数分解さて、上記の公式を使って、6乗の差を因数分解してみましょう: この因数分解を2通りで行って よって、因数分解すると、 $$x^27x30=(x10)(x3)$$ となるわけです。 因数分解の目印がないとき、 \(x^2pxq\)の因数分解は、 (1) かけて\(q\)になり、 (2) たして\(p\)になるような 2つの数\(a\) , \(b\)を求める! 3 たすきがけの因数分解 ここからは高校生向けです。
因数分解 公式 3 乗
因数分解 公式 3 乗- 因数分解の公式はよく教科書にわかりやすく載っていますが、複素数をつかった因数分解の公式はあまり載っていません。 最も簡単な例は、\(\displaystyle a^2b^2\)の因数分解です。 3乗→3乗の因数分解公式5つと例題 ~めったに使わない、四乗の公式~ $x^44x^3y6x^2y^24xy^3y^4$$=(xy)^4$ $x^44x^3y6x^2y^24xy^3y^4$$=(xy)^4$ $x^4y^4$→これ以上因数分解できない $x^4y^4=(xy)(x^3x^2yxy^2y^3)$ ~高校数学で習う難しめの公式~ $a^2b^2c^22ab2bc2ca$$=(abc)^2$ $a^3b^3c^33abc$

高校数学 因数分解 解の公式を使ってルートが登場する因数分解を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト
男と女の生まれる確率は同じじゃない – その理由は? 円周率の意味って何? – πの意味を分かりやすく説明します; 多項式の基本6|3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように,たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は,いったん解を求めることによって因数分解できるのでした. では,3次式では因数分解 因数分解2乗の公式 特に重要なのが、④の公式です。 ④の公式に \(a=y,b=y\) を代入すると①の公式になり、\(a=y,b=y\) を代入すると②の公式になり、\(a=y,b=y\) を代入すると③の公式
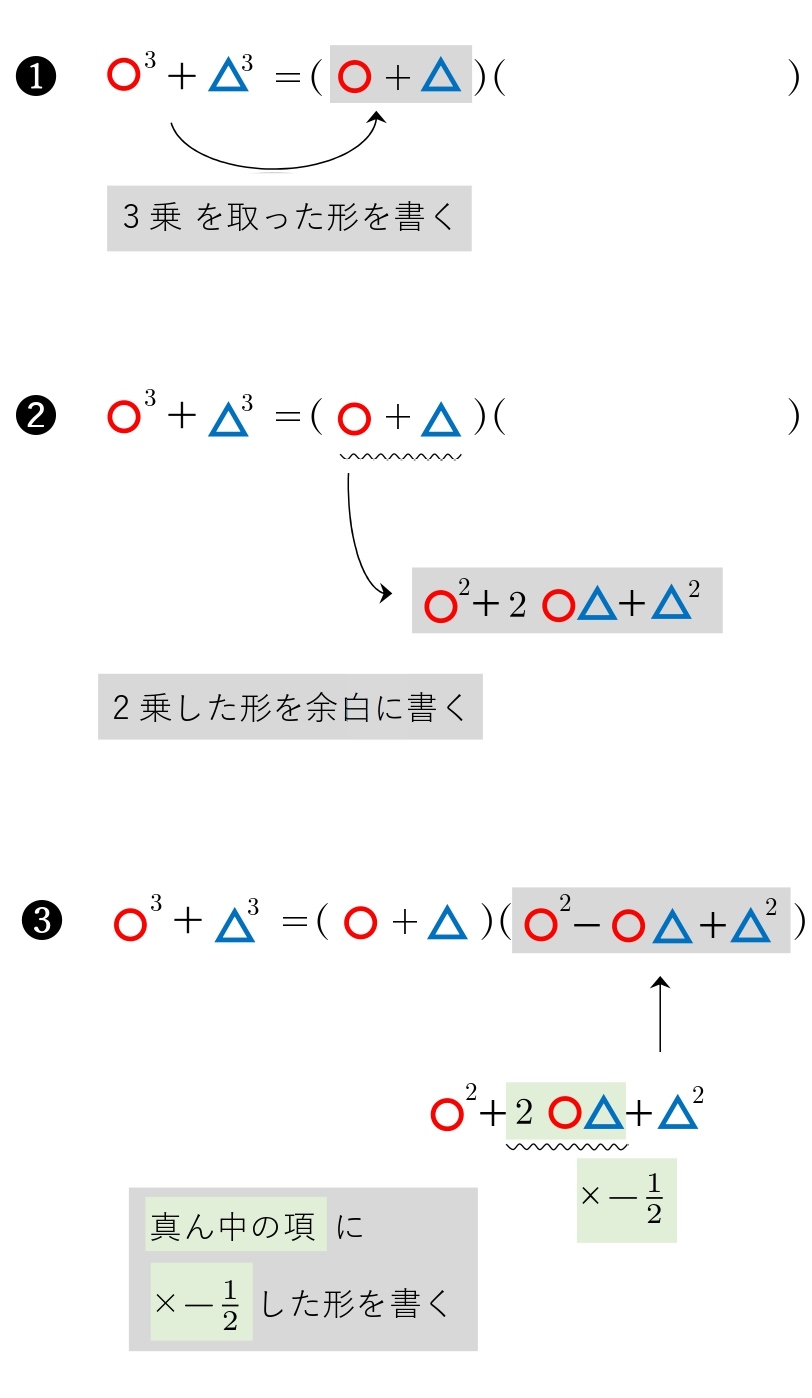
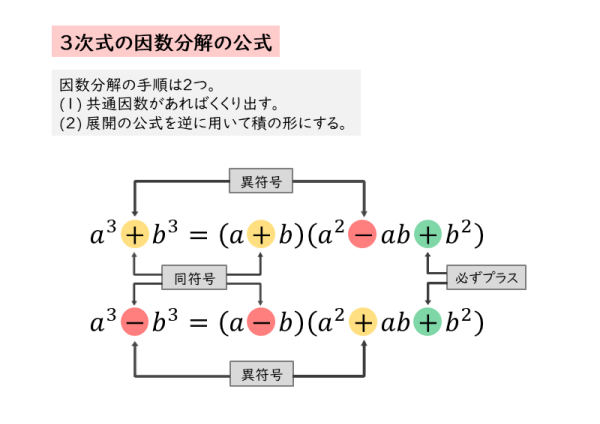
最低次の文字の次数が3次以上の時は(i) の公式を適用するか、(ii)の共通因数でくくりだすパターンが多いです。 (iv) 上記の方法でできないときは必ず( ) 2 ( ) になってくれているので、 a2 b2 = (a b)(a b)の公式を使って因数分解をする。 因数分解の解法は上記の 1 数学 質問解答3乗をふくんだ式の因数分解 パート2高校数学 数a 因数分解(質問ありがとうございました! 11 2項の式の3乗の展開公式しかし、 応用編で3乗の計算 がでてくるときがあります。 3乗の因数分解の公式は次のとおりです。 (1) a³+3a²b+3ab²+b³= (a+b)³ (2) a³−3a²b+3ab²−b³= (a−b)³ (3) a³+b³= (a+b) (a²−ab+b²) (4) a³−b³= (a−b) (a²+ab+b²) ためしに3番目と4番目の公式を使って問題を解いてみましょう。 次の式を因数分解しなさい。 問1:x³+27
因数分解 公式 3 乗のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 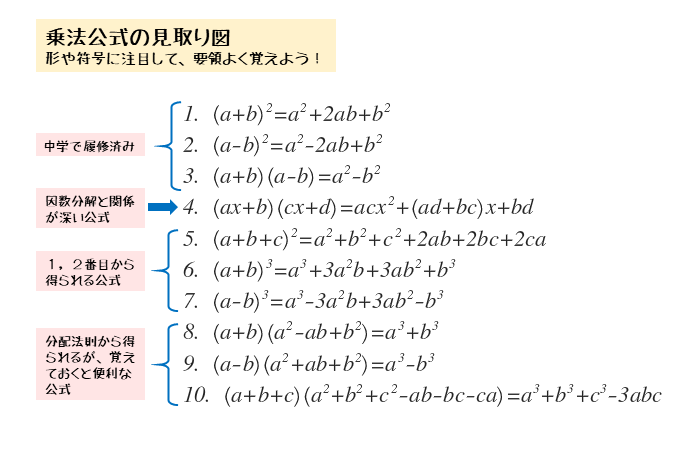 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 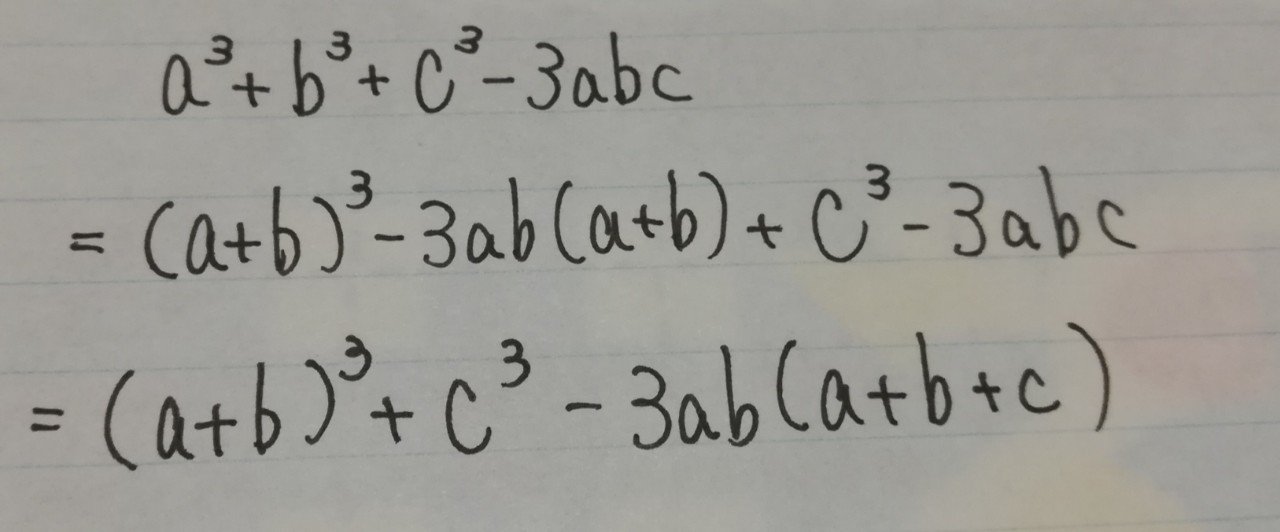 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 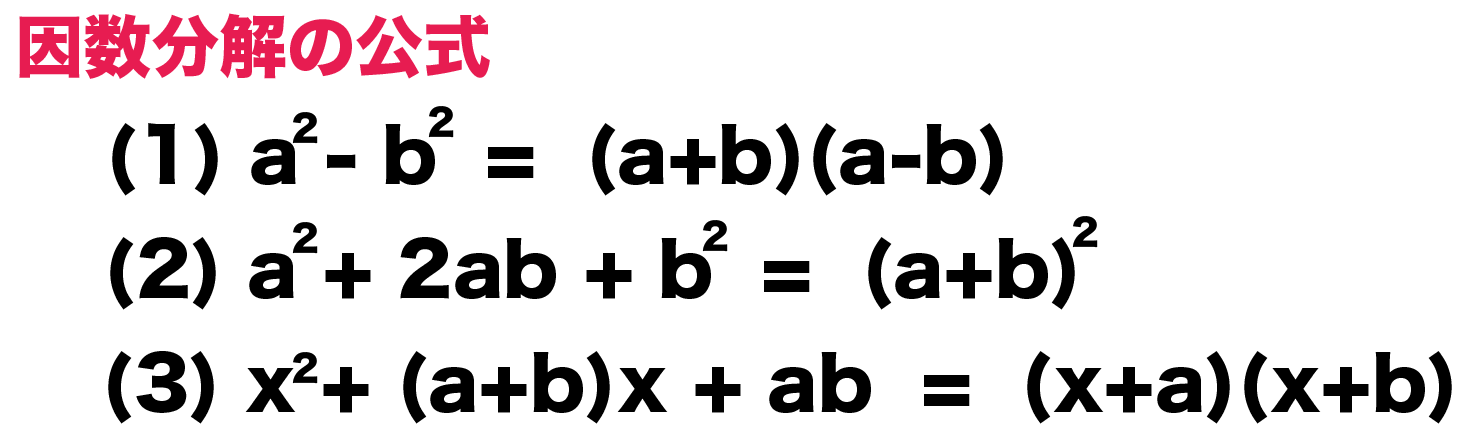 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
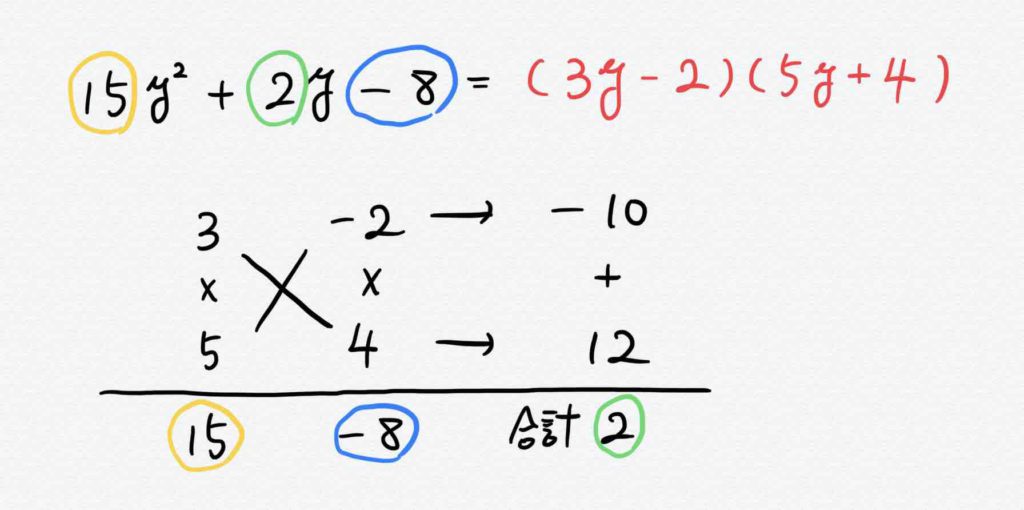 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 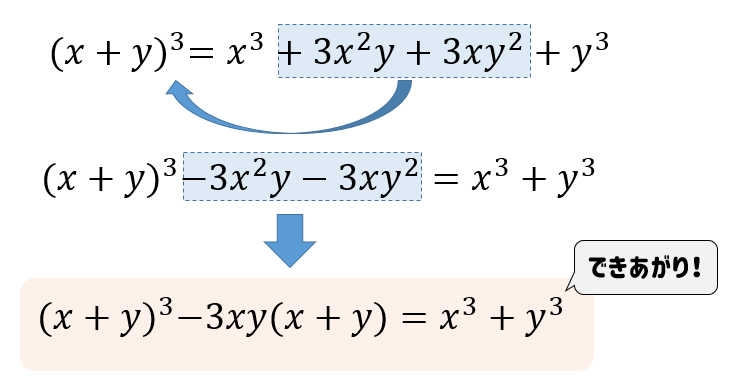 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 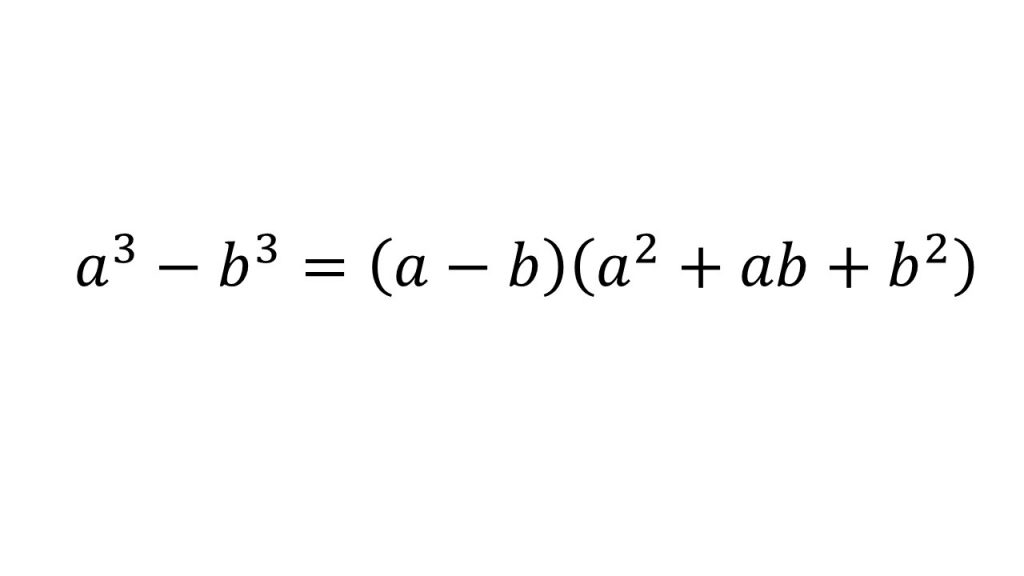 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
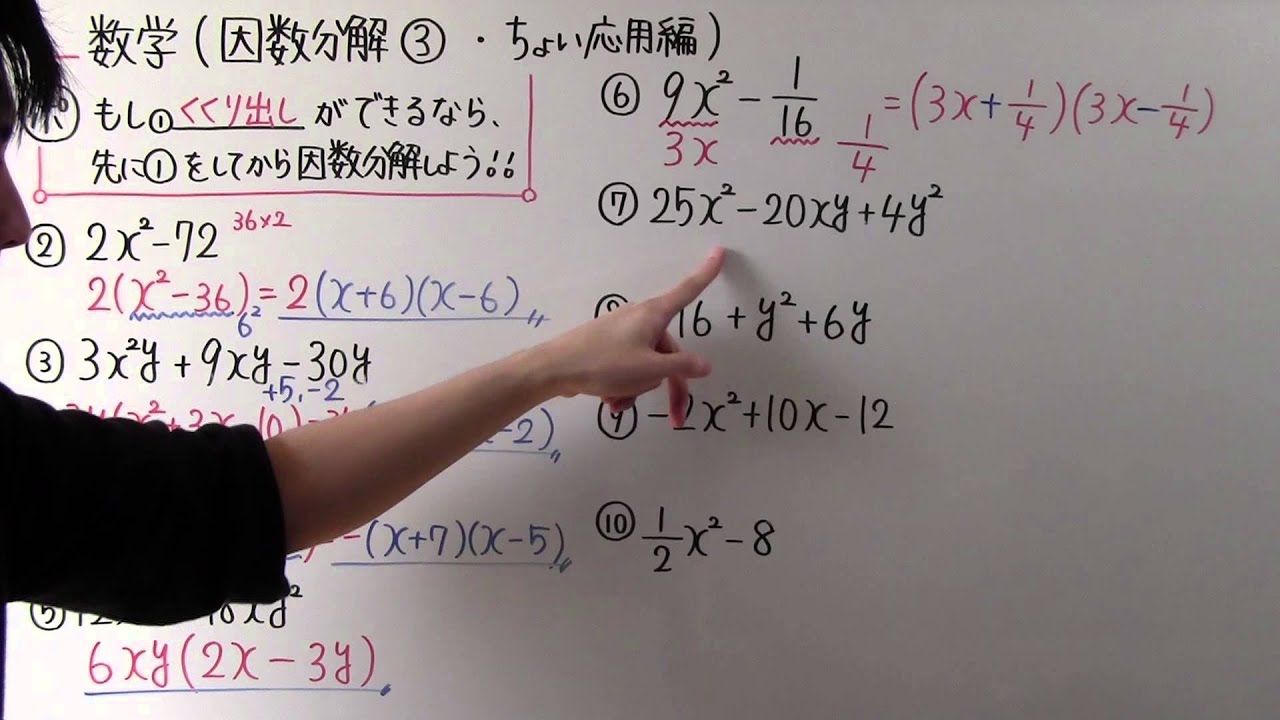 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 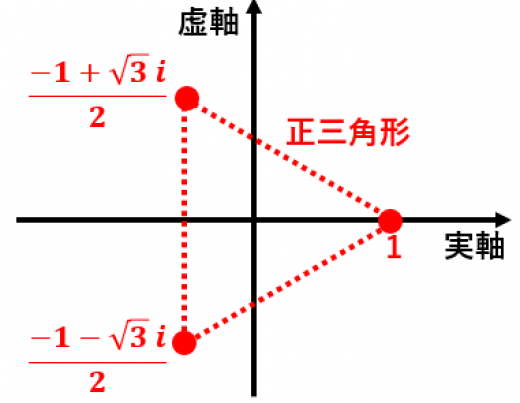 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 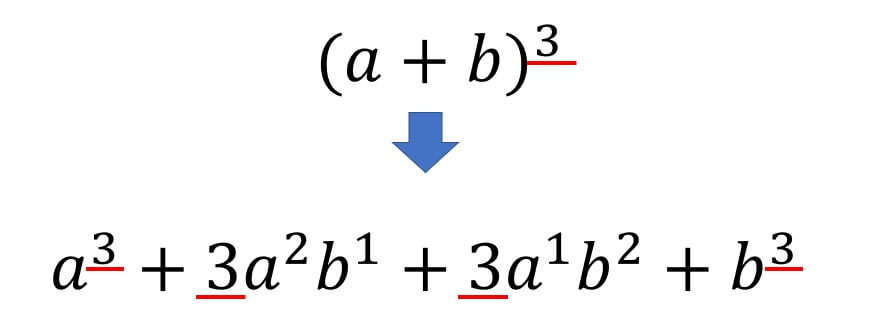 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 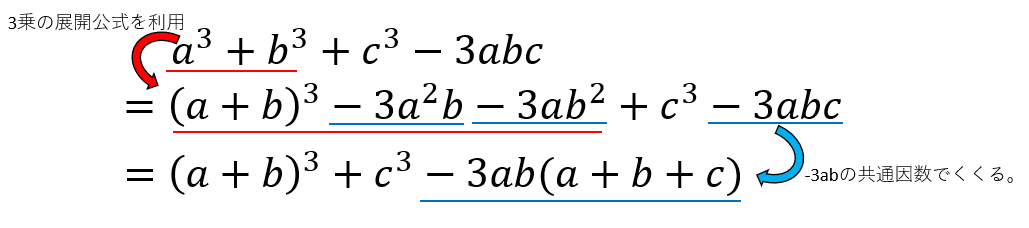 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す | 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
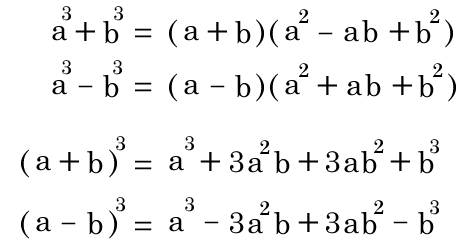 3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |  3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す |
因数分解ができると、 二次以上の方程式を解く のに役立ちます。 因数分解の公式 ここでは、因数分解の \(2\) 乗の公式および \(3\) 乗の公式を確認していきます。 2 乗の公式 二次式を因数分解する公式は以下の通りです。 この変形後の式で、1つ目と3つ目に注目してみましょう。 「3乗足す3乗」の形になっていますね。 三次式の因数分解の式が使うと、 a b c a b c が出てきます。 また、2つ目と4つ目に注目すると、 3ab 3 a b でくくれば、こちらからも a b c a b c が出てきます。 なので、まとめられそうですね。 まとめると、次のように変形できます。 (a b)3 c3 −3ab(a b)−
コメント
コメントを投稿